Kui kaugel näete meteoriiti?
>Ma saan meili.
Enamik küsib erinevat tüüpi küsimusi, millest enamikule on üsna lihtne vastata (tegelikult võiks googeldades, vihjega vihjeid) palju vastata. Kuid mõnikord saan küsimuse, millele on raskem vastata, või isegi sellise küsimuse, mille üle olen mõelnud, kuid pole kunagi jõudnud välja mõelda.
Nii et olin üsna intrigeeritud, kui sain halva lugeja Dean Lewise küsimuse meteooride kohta. 2018. aastal Perseidi meteoorivoolu ajal oli ta oma perest eemal, keda lahutas umbes 1000 kilomeetrit. Kui ta nägi meteoriiti, kas oli võimalik, et nad nägid sama kaugemast kohast?
Lühike vastus on: Jah! Pikk vastus on… matemaatika. Lahe, lõbus matemaatika.
Ja nähes, kuidas selle artikli postitamisel 2018. aasta Geminidi meteoorivoolu tipphetked täna õhtul on minu arvates asjakohane see välja mõelda.
Crash Course Astronomy: Meteorid, Meteoroids ja Meteorites, Oh My!
Kui Maa oleks täiesti tasane, siis põhimõtteliselt näeksite meteoriiti kuni Maa mis tahes servani. Niikaua kui olete maapinnast kõrgemal, kasvõi pisike, jõuab teie vaateväli teie poolel oleva planeedi iga ruutsentimeetrini, nii et iga meteoor on kõigile nähtav. Tegelikkuses ei ole õhk täiesti läbipaistev, nii et vaatate teatud vahemaa tagant nii palju sodi, et te ei näe midagi.
Maa pole aga lame. Tõsiselt! See on ümmargune. Ja õhkkond ümbritseb seda nagu kest, muutudes pikkusega õhemaks ja lõpuks välja kukkudes; see kõrgus sõltub teie ruumi määratlusest. Siiski võime natuke petta, kuna tunneme teadust: sellised meteoorid nagu duširuumid kipuvad põlema umbes 100 kilomeetri kõrgusel maapinnast. See kõrgus sõltub paljudest asjadest, sealhulgas sellest, kui suur see on meteoroidid (planeetidevahelise prahi tahked osad, mis kosmoses tiirutavad) on, kui kiiresti nad liiguvad, millise nurga all nad atmosfääri sisenevad jne. Aga nimetagem seda 100 km.
Lähim meteoor võib teile olla, kui olete otse selle all, ja siis on see 100 km otse üles (teie seniidil). Kui see põleb seniidist kaugemal, peab see olema sinust kaugemal. Kaugemal võib näha meteoriiti, see on mõistlik, seega kui see on täpselt silmapiiril.
Selle geomeetria näeb välja selline (märkus: MITTE mõõtkavasse):
wallace ja gromit needus warerabbit
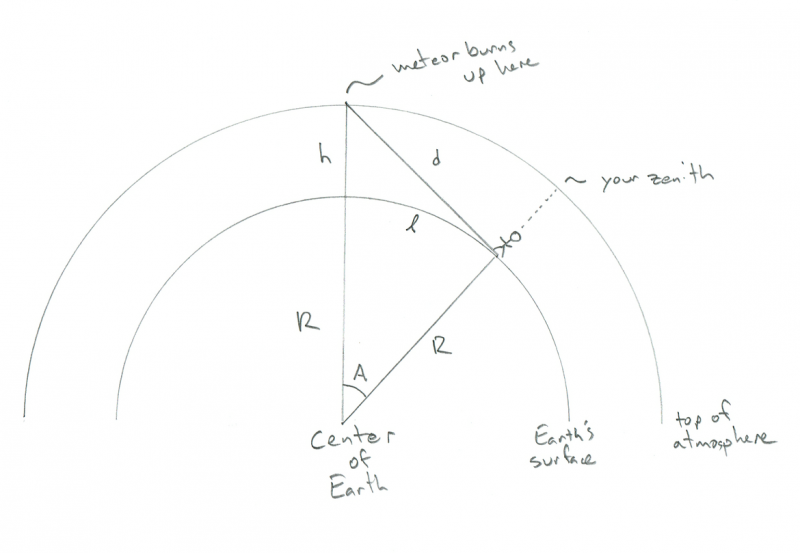
Skeem, mis näitab meteoriidi põlemist jälgiva vaatleja geomeetriat. Krediit: Phil Plait
Näete väikest pulgakuju, kes seisab kõverjoonelise Maa pinnal - oletame, et see olete teie -, mille kohal on (ka kõver) atmosfäär. Sellel diagrammil on R Maa raadius (6400 km), h on meteoriidi põlemise kõrgus (100 km) ja d on kaugus sinust meteoorini. A on nurk teie asukoha Maal ja meteoriidi asukoha vahel selle kohal ning kursiiv l (nagu pikkus) on vahemaa, mille peate läbima, et meteoor oleks otse pea kohal (ma tean, et see tundub imelik asi) tahad teada, aga kanna minuga). Kummalisel kombel saate siin arvutada kõike, mida vajate, teadmata d, aga c'mon, on lahe teada, kui kaugel on meteoor, eks?
Selle kõige võti on näha, et nurk meteoriidi, teie ja Maa keskpunkti vahel on täisnurk. Selle põhjuseks on asjaolu, et meteoor on silmapiiril teie poolt vaadatuna (või kui eelistate lõbusat kõnepruuki, siis siseringi puutujajoonel, kus R seda lõikab). See teeb kolmnurgast täisnurkse kolmnurga ja kui mäletate oma keskkooli matemaatikat, tähendab see, et leiate kõik küljed ja nurgad!
Pidage meeles Pythagorase teoreem ? Täisnurkses kolmnurgas on hüpotenuusi pikkuse ruut võrdne kahe teise külje ruutude summaga*. Meie kolmnurgas on hüpotenuus R+h ja teised küljed R ja d.
Niisiis
(R+h)2= d2+ R2
või korrutades vasakpoolset külge (kasutage FOOL ):
R2+ 2Rh + h2 = d2+ R2
Lahendage d, et näha, kui kaugel on meteoor teist. Pange tähele, et R2 on mõlemal küljel, seega tühistage need
d2= 2Rh + h2
Või
d = ruutjuur (2Rh + h2)
Noh, me teame kõiki neid numbreid! Plug-n-chug, laps:
d = ruutjuur (2 x 6400 x 100 + 10 000) = 1136 km
Ahaa! See tähendab, et kui näete silmapiiril meteoriiti, on see üle 1100 kilomeetri kaugusel! See on pikk tee ja tehniliselt kõige kaugemal näete maapinnast meteoriiti.
Leiame nüüd kursiivse l. Kõigepealt peame teadma nurka A. See nõuab teatud trigonomeetriat. On palju trig identiteete saate seda välja mõelda, kuid minu lemmik†on see, et täisnurkses kolmnurgas on nurga siinus vastaskülje pikkus jagatud hüpotenuusi pikkusega. Nii et kui saame selle suhte, võime nurga saamiseks võtta pöördsinuse (või kaarsiini).
sin (A) = d / (R + h)
nii
A = ilma-1(d / R + h)
Plug-n-chug uuesti ja ma saan A = 10 °. See on korralik tükk Maa pinnast!
Ja nüüd saame kursiivse l. Maa ümber on 360 ° ja Maa ümbermõõt on 2 x pi x raadius = 40 192 km, seega on
40 192 km / 360 ° = 112 kilomeetrit kraadi kohta
mis tähendab omakorda 10 ° = 1120 kilomeetrit. See on üsna lähedal d -le, mis pole liiga üllatav. Joonised on liialdatud, kuid tegelikult on õhukarp meie kohal Maa suurusega võrreldes väike. Kui teeksin joonised mõõtkavas, näeksite, et d ja l on tõesti üsna lähedased.
OK, miks ma olen siis kuum ja viitsinud mind leida? Algse küsimuse pärast! Kui olete pärast seda matemaatikat unustanud, siis kui kaugel võivad kaks inimest olla ja siiski sama meteoriiti näha?
Sel juhul oleks meteoor otse nende vahel ja igal nende horisondil. See geomeetria näeb välja selline:
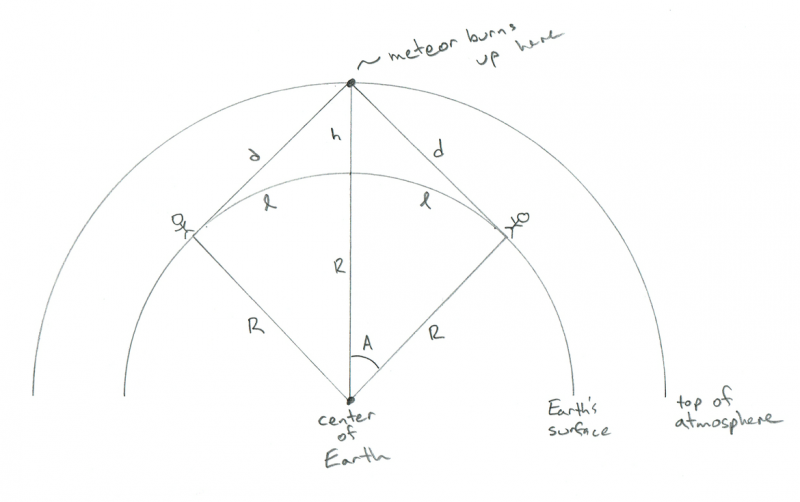
Skeem, mis näitab kahe vaatleja geomeetriat, kes jälgivad täpselt nende vahel põlevat meteoriiti. Krediit: Phil Plait
AHA! Nüüd näete, miks ma tahan! Kahe inimese vaheline kaugus on vaid 2 x l! Nüüd on meil vastus:
Kahe inimese jaoks sama meteoriidi nägemiseks ei tohi nende vahe olla suurem kui 2 x 1120 = 2240 kilomeetrit. Näiteks Washingtoni ja Denveri vaheline kaugus on üsna lähedal. Vau.
Muide, perspektiivi muutmiseks (sõna otseses mõttes) tähendab see meteoriidi seisukohast, et see võib näha 2240 kilomeetri laiust Maa lõiku (nagu DC idapoolsel maaosas ja Denver lääneosas). See on päris lahe.
Ja see viib meid tegeliku vastuseni Deani küsimusele: kui ta oleks oma perest 1000 km kaugusel, siis jah, tehniliselt näeksid nad sama meteoriiti. Kuidas oleks?
Nüüd eeldatakse jälle, et õhk on täiesti selge ja kõik see, mis tegelikult on sisuliselt võimatu. Nii et see matemaatika kujutab endast ideaalset olukorda (sealhulgas ideed, et meteoor asub täpselt nende vahel).
Olgem realistlikumad. Oletame, et meteoor põleb taevas 45 ° kõrgusel horisondi kohal mõlema vaatleja jaoks. Kui kaugel nad üksteisest oleksid? Eeldusel, et meteoor asub täpselt nende vahel, on geomeetria selline:
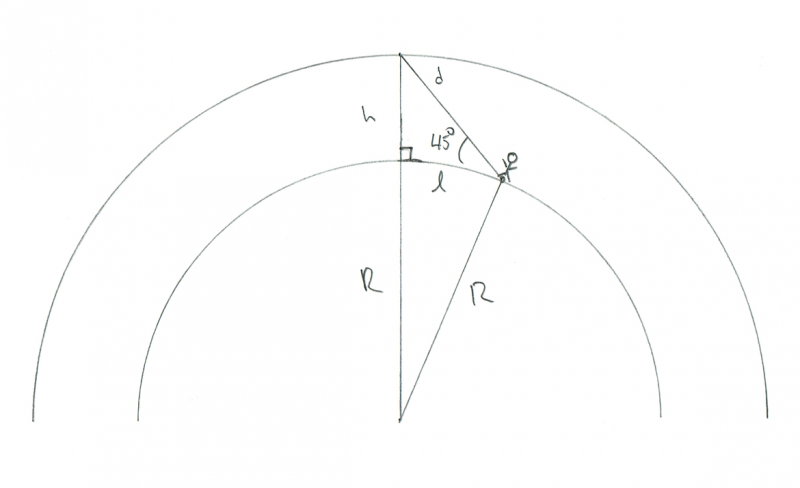
Skeem, mis näitab vaatleja geomeetriat, kui ta jälgib 45 ° horisondi kohal põlevat meteoriiti. Krediit: Phil Plait
Seda on tegelikult keerulisem lahendada, kuid ma tean veel ühte nippi: kui eeldame, et l on väike, pole Maa kõverus oluline. Näiteks kui ma tahan teada oma õue kahe puu vahelist kaugust, ei hooli ma sellest, et Maa on kõver. Nii väikese vahemaa tagant võin eeldada, et see on tasane. Teeme selle oletuse siin.
Sel juhul on meil veel üks täisnurkne kolmnurk, kuid seekord on õige nurk meteoriidi all. Märkisin selle skeemil isegi väikese ruudukujulise märkega. Nii et kui see on 90 ° nurk ja meie nurk meteoriidi suhtes on 45 °, siis viimane nurk (meteoorist vaatlejani) on samuti 45 °. See tähendab, et see peab olema võrdkülgne kolmnurk, nii et l ja h on samad! Kuna me teame, et h on 100 km, siis peab seda tegema ka l.
Ja see tähendab, et meie kahe vaatleja vaheline kaugus on kaks korda suurem ehk 200 km.
kunagi ammu lääne reitingus
Muide, sel juhul on kaugus meteoorist umbes 141 km. Jätan selle kinnitamise lugejana harjutuseks.
Põhimõtteliselt tähendab see seda, et kui teate, kui kõrgel on meteoor horisondist ja kui kõrgel see põles, saate arvutada selle kauguse (või kui teate kaugust, saate selle kõrguse). See käivitus on siiski üsna keeruline ja ma arvan, et olen teile täna piisavalt matemaatikat visanud.
Kuid on lahe mõelda, et natuke gümnaasiumi matemaatikat võib olla nii lõbus rakendus. Ja ma tunnistan, et on poeetiline ja romantiline teada, et seni, kuni lahusolek pole liiga kaugel, on võimalik lasta lasketähe nägemist kellegi teisega. Milline armas mõte.
* Sisse Võlur Oz , hernehirmutis sai sellest valesti aru pärast tal oli aju.
† / muidugi Mul on lemmik trig identiteet. Mis on sinu?